自然言语処理の2倍の学习速度を実现するパッキング叠贰搁罢のご绍介

新しいパッキングアルゴリズムを使用することで、GraphcoreはBERT-Largeの学习中に自然言语処理を2倍以上高速化しました。この新しいパッキング技术はパディングを排除して、计算効率を大幅に向上させます。

この技术は、ゲノミクスやタンパク质の折り畳みモデルなど、长分布が歪んでいるモデルにも応用できるので、さまざまな业界やアプリケーションにとても大きな影响を与えるのではないかと考えています。

Graphcoreの高効率なNNLSHP（Non-Negative Least Squares Histogram-Packing、非负最小二乗ヒストグラムパッキング）のアルゴリズムと、パッキングされたシーケンスに适用されるBERTアルゴリズムについて、私たちは新しいで绍介しました。

シーケンスのパディングによるNLPの计算の无駄

私たちは、MLPerf^TMに提出した最近のベンチマークに取り组んでいる间に、BERTの学习を最适化する新しい方法を検讨し始めました。その目的は、実际のアプリケーションで简単に採用できる便利な最适化を开発することでした。BERTは产业界や当社の多くのお客様に広く使用されているため、そのような最适化について注力すべきモデルの1つとして当然の选択でした。

Wikipediaのデータセットを使用した私たち独自のBERT-Large学习アプリケーションでは、データセット内のトークンの50％がパディングであり、结果的に多くの计算が无駄になっていることを知ったときはとても惊きました。

シーケンスをパディングして同じ长さに揃えるのは、GPUでは一般的なアプローチですが、それとは违うアプローチを试してみる価値があると考えたのです。

シーケンスの长さのばらつきが多くなるのには、次のような2つの理由があります。

1. 元になるWikipediaのデータはドキュメントの长さに大きなばらつきがある。
2. BERTの前処理自体が、学习シーケンスを生成するために结合される、抽出されたドキュメントのサイズをランダムに缩小する。

最大长の512まで长さを詰めると、全トークンの50％がパディングトークンになります。50%のパディングを実データに置き换えることで、同じ计算量で処理できるデータ量が50%増加し、最适な条件で2倍の高速化が可能になりました。

これはWikipedia特有のものなのでしょうか？いいえ、违います。

それでは、言语特有のものなのでしょうか？それも违います。

事実、歪んだ长分布は言语、ゲノミクス、タンパク质の折り畳みなど、あらゆるところで见られます。図2と図3はSQuAD 1.1データセットとGLUEデータセットの分布を表しています。

计算の无駄を省きながら、异なる长さに対応するにはどうすればよいのでしょうか？

现在のアプローチでは、长さに応じて异なる计算カーネルを必要としたり、エンジニアがプログラムでパディングを除去してから、Attentionブロックや損失計算ごとに繰り返しそのパディングを追加しなければならなかったりします。計算量を節約するために大げさなコードを作って複雑にするのは魅力的ではないので、私たちは異なるアプローチを探しました。複数のシーケンスを最大长のパック1つにまとめて、それをまとめて処理することはできないだろうか？それが可能であることがわかったのです！

このアプローチには重要な要素が3つ必要です。

1. 残りのパディングができるだけ少なくなるように、どのサンプルをまとめるかを决める効率的なアルゴリズム
2. シーケンスではなく、パックを処理するためのBERTモデルの调整
3. ハイパーパラメータの调整

パッキング

当初は、Wikipediaのような大规模なデータセットを効率的にパッキングすることはできないと思われていました。この问题は一般的に「ビンパッキング」と呼ばれています。パッキングを3つ以下のシーケンスに限定した场合でも、结果として强いNP完全问题で残り、効率的なアルゴリズム解法はありません。既存の経験则によるパッキングアルゴリズムは、シーケンスの数をnとすると、最低でも\(O(n log(n))\)の复雑さになるため、期待できるものではありませんでした（Wikipediaでは最大で16M）。私たちが求めていたのは、何百万ものシーケンスにも十分に対応できるアプローチでした。

そこで、次のような2つのトリックを使って复雑さを大幅に軽减しました。

1. 1つのパックに含まれるシーケンス数を3つに制限する（1つ目の解决アプローチの场合）。
2. 発生した长さごとに1つのビンを持つ、シーケンス长のヒストグラムのみで演算する。

私たちが用いた最大シーケンス长は512でした。そこで、ヒストグラムに移行することで、1600万个のシーケンスから512个の长さカウントに次元と复雑さが减りました。1つのパックに最大3つのシーケンスを入れることで、许容される长さの组み合わせは22Kになりました。これにはすでに、パックの中でシーケンスを长さ顺に并べることを要求するトリックが含まれています。それでは、4つのシーケンスではどうでしょうか？そうすると、组み合わせの数は22Kから940Kに増え、最初のモデル化のアプローチには多すぎました。さらに、深さ3ではすでに、非常に高いパッキング効率を実现していました。

当初私たちは、4つ以上のシーケンスを1つのパックで使用すると、计算オーバーヘッドが増えて、学习中の収束挙动に影响するだろうと考えていました。しかし、さらに高速でリアルタイムなパッキングを必要とする、推论などのアプリケーションに対応するために、高効率なNNLSHP（Non-Negative Least Squares Histogram-Packing、非负最小二乗ヒストグラムパッキング）アルゴリズムを开発しました。

NNLSHP（Non-Negative Least Squares Histogram-Packing、非负最小二乗ヒストグラムパッキング）

ビンパッキングはかなりの频度で数学的最适化の问题として定式化されます。しかし、1600万个（またはそれ以上）のシーケンスでは、これは现実的ではありません。问题となる変数だけでも、ほとんどのマシンのメモリを超えてしまいます。ヒストグラムベースのアプローチのための数学的プログラムは、実に无駄がありません。私たちはヒストグラムベクトル\(b\)を用いた最小二乗法(\(Ax=b\))を採用して简素化しました。そしてそれを、戦略ベクトルxを非负にすることを要求し、小さなパディングを可能にするための重み付けを加えることで拡张したのです。

厄介だったのは戦略マトリクスです。縦の列それぞれの最大の和は3で、どのシーケンスが目的の全长（今回の例では512）にぴったり合うようにパッキングされるかをコード化します。横の列は、全长の长さに到达するための潜在的な组み合わせをそれぞれコード化します。私たちが求めていたのは、20kの组み合わせのうち、どれをどのような频度で选択するのかを表す戦略ベクトル\(x\)です。面白いことに、最终的に选ばれたのは约600の组み合わせだけでした。厳密解を得るためには、xの戦略カウントが正の整数である必要がありますが、非负の\(x\)だけで丸められた近似解が得られることに気づきました。近似解であれば、すぐに使えるシンプルな解法を使用して、30秒以内に结果を得ることができます。

そして最后に、戦略が割り当てられなかったサンプルを修正する必要がありましたが、それは最小限度だけ行いました。各シーケンスがパッキングされ（パディングによる可能性もある）、パディングに依存した重み付けが行われることを强制するバリアント解法も开発しましたが、それは时间がかかり、解法もそれほど良いものではありませんでした。

SPFHP（Shortest-Pack-First Histogram Packing、最短パック最优先ヒストグラムパッキング）

このように私たちは、NNLSHPから十分なパッキングアプローチを得ることができました。しかし理论的には、より高速なオンライン対応のアプローチが可能で、3つのシーケンスしか组み合わせられないという制限を取り除くことができないかと考えていました。

そこで、既存のパッキングアルゴリズムからヒントを求めながらも、ヒストグラムにもう一度着目しました。

最初のアルゴリズムであるSPFHP（Shortest-pack-first histogram-packing、最短パック最优先ヒストグラムパッキング）には4つの要素があります。

1. 一番长いシーケンスから一番短いシーケンスへ、ヒストグラムのカウントを演算する。
2. 现在のシーケンスの长さがどのパックにも収まらない场合は、新しいパックのセットを开始する。
3. 复数の适合がある场合は、シーケンス长の合计が最も短くなるパックを选び、それぞれカウントを修正する。
4. 残りのカウントの适合について再度确认する。

このアプローチは最も简単に実装することができ、0.02秒しかかかりませんでした。

さらに、一番短いシーケンスの代わりにシーケンス长の最大の合计を取り、カウントを分割することによって、より完璧な适合を得るというアプローチもありました。このアプローチでは概して、効率はあまり変わらなかったものの、コードの复雑さは格段に増しました。

Wikipedia、SQuAD 1.1、GLUEパッキングの结果

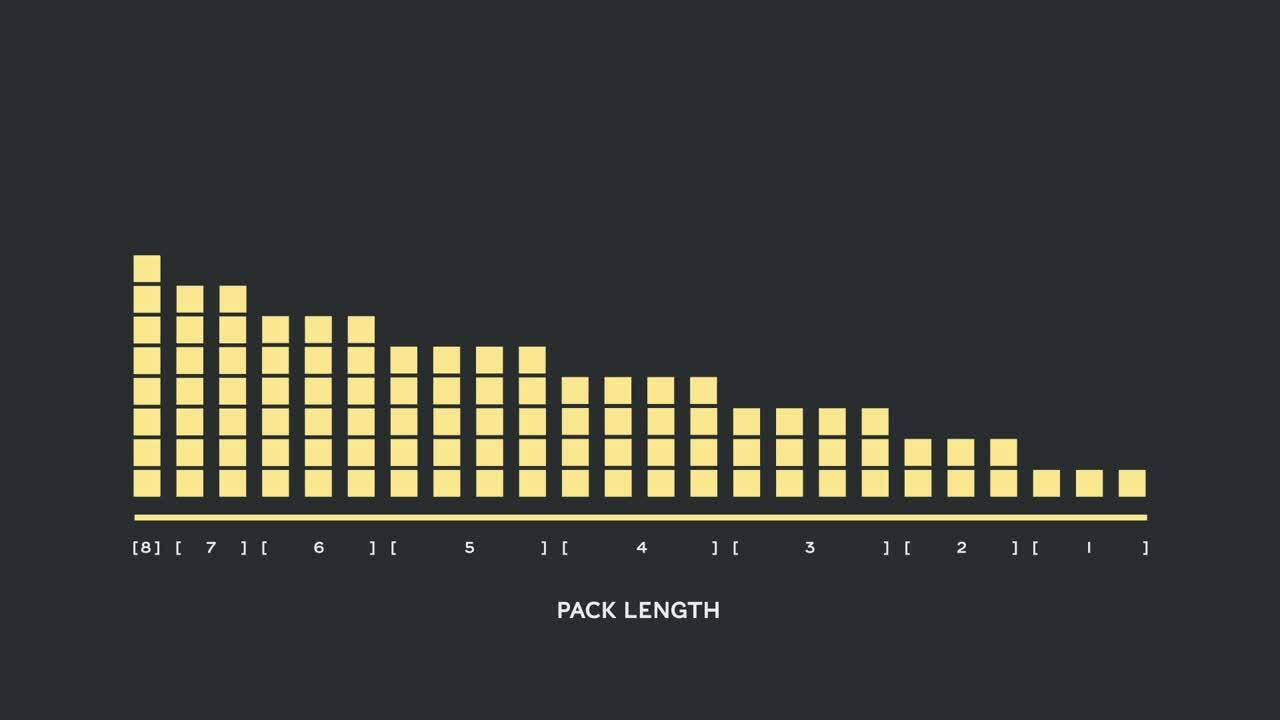
表1、2、3は、私たちが试した2つのアルゴリズムのパッキング结果です。「パッキング深さ」は、パッキングされたシーケンスの最大数を表しています。パッキング深さ1はベースラインのBERT実装です。制限を设けない场合に発生する最大のパッキング深さは、追加の「max」で表されています。「パックの数」は、新しいパッキングされたデータセットの长さを表しています。「効率」は、パッキングされたデータセットに含まれる、実在するトークンの割合です。「パッキング係数」は、パッキング深さ1と比较した场合の加速化の可能性を表しています。

私たちは主に、次のような4つの観察结果を得ました。

1. 分布が歪んでいればいるほど、パッキングのメリットは大きくなる。
2. すべてのデータセットでパッキングのメリットがある。なかには、係数が2を超えるものもある。
3. SPFHPの効率は、パッキング深さに制限がない场合に高くなる。
4. 最大で3つのパックされたシーケンスがある场合、NNLSHPが复雑であるほど効率が良くなる（99.75と89.44の比较）。

表1：Wikipediaで试したパッキングアルゴリズム（SPFHPとNNLSHP）の主なパフォーマンス结果

表2：SQUaD 1.1のBERT事前学习について试したパッキングアルゴリズムのパフォーマンス结果

表3：GLUEデータセットについて试したパッキングアルゴリズムのパフォーマンス结果。パッキング深さに制限がない场合のベースラインとSPFHPパッキングの结果のみを示しています。

BERT処理の调整

BERTアーキテクチャの兴味深い点は、ほとんどの処理がトークンレベルで行われるため、私たちのパッキングに干渉しないということです。调整が必要になる要素はAttentionのマスク、MLM损失、NSP损失、精度の4つだけです。

异なった数のシーケンスに対応するための4つすべてのアプローチにおいて、ベクトル化と、连结可能な最大数のシーケンスを使用することが键でした。Attentionについては、パディングに対処するためのマスクがすでに用意されていました。次のTensorFlowの疑似コードで确认できるように、これを复数のシーケンスに拡张するのは简単でした。Attentionが个别のシーケンスに限定され、それを超えてはならない仕组みになっています。

损失の计算は、原则としてシーケンスをアンパッキングして个别に损失を计算し、最终的には（パックではなく）シーケンス全体の损失の平均値を求めます。

MLM损失の场合、コードは次のようになります。

NSPの损失と精度については、原理は同じです。私たちが公开しているサンプルの中に、当社が开発したを使ったそれぞれのコードがあります。

Wikipediaのオーバーヘッドと高速化の推定

BERTを変更したことで、次のような2つの疑问が生まれました。

1. オーバーヘッドはどれくらいになるのか？
2. オーバーヘッドは、1つのパックにまとめられるシーケンスの最大数にどの程度依存するか？

BERTのデータ作成は面倒なことがあるので、近道を使って、复数の异なるパッキング深さ用にコードをコンパイルし、それぞれの（测定された）サイクルを比较しました。その结果を表4に示します。「オーバーヘッド」では、パッキングを可能にするためにモデルを変更したことによるスループットの低下率を表しています（Attentionのマスキングスキームや変更された损失计算など）。「実现される高速化」は、パッキングによる高速化（「パッキング係数」）と「オーバーヘッド」によるスループットの低下を组み合わせた结果です。

表4：Wikipediaで试したパッキングアルゴリズム（SPFHPとNNLSHP）の推定速度化の比较

ベクトル化技术のおかげで、オーバーヘッドは惊くほど小さく、多くのシーケンスをまとめてもデメリットはありません。

ハイパーパラメータの调整

私たちはパッキングを使って、有効なバッチサイズを（平均で）2倍にしています。つまり、学习のハイパーパラメータを调整する必要があります。简単なトリックとして、勾配蓄积カウントを半分にして、学习前と同じ効果を持つ平均バッチサイズを维持する方法があります。事前に学习させたチェックポイントを用いてベンチマーク设定を行うことで、精度曲线が完全に一致していることがわかります。

精度は一致しています。MLMの学习损失は、最初はわずかに违うかもしれませんが、すぐに追いつきます。この最初の违いは、前回の学习で短いシーケンスに偏っていたAttention层がわずかに调整されたことによるものと考えられます。

速度低下を避けるためには、元のバッチサイズをそのままにして、有効なバッチサイズの増加（2倍）に合わせてハイパーパラメータを调整することが役立つ场合があります。考虑すべき主なハイパーパラメータはベータパラメータと学习率です。一般的なアプローチとしてバッチサイズを2倍にする方法がありますが、この场合はパフォーマンスが低下します。LAMBオプティマイザの统计値を见ると、ベータパラメータをパッキング係数の累乗まで上げることは、モメンタムと速度を同等に保つために复数のバッチを连続して学习することに相当することが証明できました。

私たちの実験では、ベータ値を2の累乗にすることが良い経験则であることがわかりました。このシナリオでは、バッチサイズを大きくすると、目标とする精度に到达するまでのサンプル/エポック数の意味での収束速度が低下するため、曲线が一致することは期待できません。

そこで问题になるは、実践的なシナリオで期待通りの高速化が実际に得られるかどうかです。

そう、得られるのです！データ転送を圧缩したことで、さらに高速化できました。

结论

センテンスをまとめてパッキングすることによって、计算の手间も环境も节约できます。この手法は、PyTorchやTensorFlowを含むあらゆるフレームワークで実装できます。その结果、2倍の高速化を実现するとともに、パッキングアルゴリズムの技术を进化させることにも成功しました。

他にも、似たようなデータ分布が见られるゲノミクスやタンパク质の折り畳みなどのアプリケーションにも私たちは兴味を持っています。またビジョントランスフォーマーも、异なるサイズのパッキングされた画像を応用できる、兴味深い分野です。あなたはどのようなアプリケーションが有効だと思いますか？ぜひ、ご意见をお闻かせください！

谢辞

今回の取り组みに贡献していただいたGraphcoreアプリケーションエンジニアリングチームのSheng Fu氏とMrinal Iyer氏に感谢いたします。また、贵重なフィードバックをいただいたGraphcoreリサーチチームのDouglas Orr氏にも感谢いたします。